Механические колебания и волны краткая теория. Механические колебания и волны Раздел колебания и волны
Если посмотреть на пшеничное поле в ветреную погоду, то мы увидим, что оно «волнуется», что вдоль него что-то перемещается. Не ясно что, ведь стебли остаются на месте. Они лишь наклоняются, выпрямляются, снова наклоняются и т.д. Если взять шнур и закрепить один его конец, а другой привести в колебательное движение, то мы увидим, что вдоль шнура «бежит» волна. Если мы бросим камень в воду, то вокруг места падения камня «пойдёт круги». Эти круги – тоже волны.
Источниками волн являются колебания. Колеблются стебли растений, деформируемые ветром, колеблются частицы воды, колеблется конец шнура. А колебания, возникшие в одном месте, передаются другим частицам. То, что мы называем волной, и есть распространение колебаний от точки к точке, от частицы к частице.
Моделью образования волны в шнуре может служить цепочка шариков, имеющих массу, между которыми действует сила упругости. Вообразим, что между шариками расположены маленькие пружинки.
Пусть шарик 1 отведен вверх и отпущен. Пружинка, связывающая его с шариком 2, при этом растянется, возникнет сила упругости, которая действует не только на шарик 1, но и на шарик 2. Следовательно, начнёт колебаться и шарик 2. Это приведёт к деформации следующей пружинки, так что начнёт совершать колебания и шарик 3 и т.д.
Поскольку у всех шариков одинаковые массы и силу упругости, то все шарики будут колебаться – каждый около своего положения равновесия – с одинаковыми периодами и одинаковыми амплитудами. Однако все шарики обладают инертностью (так как у них есть масса), поэтому колебания шариков начнутся не одновременно, поскольку на изменение их скорости требуется время. Поэтому 2-я точка начнёт колебаться позже, чем 1-я, 3-я позже, чем 2-я, 4-я позже, чем 3-я и т.д.
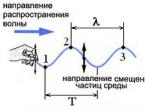
Если наблюдать за любой точкой шнура, мы увидим, что каждая точка совершает колебания с тем же периодом Т. Хотя все точки шнура колеблются с одинаковой частотой, эти колебания «смещены» относительно друг друга во времени. Именно вследствие этого смещения во времени и возникает волна. Например, колебания точки 2 отстают от колебаний точки 1 на четверть периода . А колебания точки 3 отстают от колебаний точки 2 на один целый период Т. Отсюда следует важный вывод: точки 2 и 3 движутся одинаково.
Расстояние между ближайшими точками волны, которые движутся одинаково, называется длиной волны и обозначается λ .
Итак, механические волны – это механические колебания, распространяющиеся в пространстве с течением времени.
Скорость волны
За время, равное одному периоду Т, каждая точка среды совершила одно колебание и, значит, вернулась в то же самое положение. Следовательно, волна сместилась в пространстве как раз на одну длину волны. Таким образом, если обозначить скорость распространения волны υ , получим, что скорость волны
λ = υ Т
Так как Т = 1/ν , тогда получим, что скорость волны, длина волны и частота волны связаны соотношением
υ = λ ν
Что переносят волны?
В приведённые примерах видно, что вещество не перемещается вдоль направления распространения волны, т.е. волны не переносят вещество
.
Однако волны переносят энергию
:
ведь волна – это колебание, распространяющиеся в пространстве, а любые колебания обладают энергией.
Колебания – это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени. Если колебательный процесс распространяется в пространстве с течением времени, то говорят о распространении волн.
Колебательные движения часто встречаются в природе и технике: колеблются деревья в лесу, струны музыкальных инструментов, поршни двигателя, голосовые связки, сердце и т.д. Колебательные движения происходят в жизни – землетрясения, приливы и отливы, сжимание и расширение нашей Вселенной.
Колебания возникают в системах всегда, если эти системы обладают устойчивыми положениями равновесия. При отклонении от положения равновесия возникает «возвращающая» сила, которая пытается вернуть систему в положение равновесия. Так как телам присуща инертность, то они «проскакивают» положение равновесия и тогда отклонение происходит в противоположном направлении. И тогда процесс начинает периодически повторяться.
В зависимости от физической природы различают механические и электромагнитные колебания . Однако колебания и волны независимо от их природы описываются количественно одними и теми же уравнениями.
Механические колебания – это такие движения тел, при которых через равные интервалы времени координаты движущегося тела, его скорость и ускорение принимают исходные значения.
Основные виды колебаний
1. Свободные
2. Вынужденные
3. Автоколебания
Свободные колебания
Свободные колебания – это колебания, возникающие в системе под действием внутренних сил после того, как систему вывели из положения равновесия. То есть такие колебания происходят только за счёт запаса энергии, сообщённого системе.
Условия возникновения свободных колебаний:
1.
Система находится вблизи положения устойчивого равновесия (для возникновения «возвращающей» силы);
2.
Трение в системе должно быть достаточно мало (иначе колебания быстро затухнут или вообще не возникнут).
Вынужденные колебания
Вынужденные колебания – это колебания, возникающие под действием внешних периодически изменяющихся сил.
Отличие от свободных колебаний:
1.
Частота вынужденных колебаний всегда равна частоте периодической вынуждающей силы.
2.
Амплитуда вынужденных колебаний не уменьшается со временем, даже если в системе присутствует трение. Поскольку потери механической энергии восполняются за счёт работы внешних сил.
Автоколебания
Автоколебания – это незатухающие колебания, которые могут существовать в системе без воздействия на неё внешних периодических сил. Такие колебания существуют за счёт поступления энергии от постоянного источника (которым обладает система) и регулируется самой системой.
К автоколебательным системам относятся: часы с маятником, электрический звонок с прерывателем, наше сердце и лёгкие и т.д.
Особенности автоколебаний:
1.
Частота автоколебаний равна частоте свободных колебаний колебательной системы и не зависит от источника энергии (отличие от вынужденных колебаний)
.
2.
Амплитуда автоколебаний не зависит от энергии, сообщённой системе, а устанавливается самой системой (отличие от свободных колебаний)
.
Гармонические колебания
Колебания, при которых смещение зависит от времени по закону косинуса или синуса, называют гармоническими.
Уравнение гармонического колебания
х = X max cosωt
Величины характеризующие колебательные движения
Амплитуда
Амплитуда колебаний – максимальное значение величины, которая испытывает колебания по гармоническому закону.
Физический смысл X max – максимальное значение смещения тела от положения равновесия при гармонических колебаниях.
Период и частота
Период гармонического колебания Т – это время одного полного колебания, то есть промежуток времени, через который движение полностью повторяется.
Единица измерения периода [Т ] = 1с
Частота колебаний ν – это число полных колебаний N, совершаемых телом за единицу времени t.
Единица измерения частоты [ν ] = 1 Гц = 1/с
Циклическая частота колебаний
Циклическая частота колебаний ω – это число полных колебаний, совершаемых за 2π секунд.
Единица измерения циклической частоты [ω ] = 1 рад/с
График гармонического колебания
Пример
Колебательным движением называется всякое движение или изменение состояния, характеризуемое той или иной степенью повторяемости во времени значений физических величин, определяющих это движение или состояние. Колебания свойственны всем явлениям природы: пульсирует излучение звезд; с высокой степенью периодичности вращаются планеты Солнечной системы; ветры возбуждают колебания и волны на поверхности воды; внутри любого живого организма непрерывно происходят разнообразные, ритмично повторяющиеся процессы, например, с удивительной надежностью бьется человеческое сердце.
В физике выделяются колебания механические и электромагнитные. С помощью распространяющихся механических колебаний плотности и давления воздуха, воспринимаемых нами как звук, а также очень быстрых колебаний электрических и магнитных полей, воспринимаемых нами как свет, мы получаем большое число прямой информации об окружающем мире. Примерами колебательного движения в механике могут быть колебания маятников, струн, мостов и т.д.
Колебания называются периодическими , если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени. Простейшим типом периодических колебаний являются гармонические колебания. Гармоническими называются колебания, при которых изменение колеблющейся величины со временем происходит по закону синуса (или косинуса):
где x – смещение от положение равновесия;
А – амплитуда колебания – максимальное смещение от положения равновесия;
-
циклическая частота;
-
начальная фаза колебания;
-
фаза колебания; она определяет смещение
в любой момент времени, т.е. определяет
состояние колебательной системы.
В
случае строго гармонических колебаний
величины А,
и
не зависят от времени.
Циклическая
частота
связана с периодом Т колебаний и частотой
соотношением:
(2)
Периодом Т колебаний называется наименьший промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебания.
Частотой
колебаний
называется число полных колебаний,
совершаемых за единицу времени, измеряется
в герцах (1 Гц = 1
).
Циклическая
частота
численно
равна числу колебаний, совершаемых за
2
секунд.
Колебания, возникающее в системе, не подверженной действию переменных внешних сил, в результате какого-либо начального отклонения этой системы от состояния устойчивого равновесия, называются свободными (или собственными).
Если система консервативная, то при колебаниях не происходит рассеяния энергии. В этом случае свободные колебания называются незатухающими .
Скорость
колебания точки определим как производную
от смещения по времени:
(3)
Ускорение
колеблющейся точки равно производной
от скорости по времени:
(4)
Уравнение (4) показывает, что ускорение при гармонических колебаниях – переменно, следовательно, колебание обусловлено действием переменной силы.
Второй
закон Ньютона позволяет в общем виде
записать связь между силой F и ускорением
при прямолинейных гармонических
колебаниях материальной точки с массой
:
где
,
(6)
к – коэффициент упругости.
Таким образом, сила, вызывающая гармонические колебания, пропорциональна смещению и направлена против смещения. В связи с этим можно дать динамическое определение гармонического колебания: гармоническим называется колебание, вызываемое силой, прямо пропорциональной смещению х и направленной против смещения.
Возвращающей силой может быть, например, сила упругости. Силы, имеющие иную природу, чем упругие силы, но также удовлетворяющие условию (5), называются квазиупругими .
В
случае прямолинейных колебаний вдоль
оси х ускорение
равно:
.
Подставив
это выражение для ускорения
и значение силы
во второй закон Ньютона, получимосновное
уравнение прямолинейных гармонических
колебиний:
или 
(7)
Решением этого уравнения является уравнение (1).
100. Колебательным процессом (колебанием) называется такое изменение состояния системы, при котором значения параметров состояния последовательно отклоняются то в одну, то в другую сторону от некоторого значения.
101. Свободные колебания - это колебания, которые совершаются под действием внутренних сил, пропорциональных смещению и направленных к положению равновесия. Они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.
102. Гармоническими называются колебания, при которых величины, описывающие систему, изменяются по закону синуса или косинуса. Этими величинами могут быть: координата точки, энергия, напряжённость электрического поля, индукция магнитного поля, скорость и т.д.
103. Уравнение гармонических колебаний:
где х - значение изменяющейся величины в данный момент времени, х m - амплитуда колебаний, ‑ циклическая частота, 0 - начальная фаза.
104. Амплитуда колебаний - это модуль максимального отклонения изменяющейся величина от положения равновесия.
105. Частота - это число колебаний за единицу времени (обычно за секунду). В системе СИ частота измеряется в герцах (Гц).
106. Циклическая частота - это число колебаний за 2 секунд. В системе СИ циклическая частота измеряется в с -1 .
107. Период колебаний T - это время, за которое совершается одно полное колебание. В системе СИ период измеряется в секундах (с).
108. Связь периода, частоты и циклической частоты колебаний
109. Значение выражения (t + 0), стоящего под знаком косинуса или синуса в уравнении гармонических колебаний и определяющего при постоянной амплитуде состояние колебательной системы в данный момент времени, называется фазой колебаний. Фаза колебаний в системе СИ измеряется в радианах (рад).
110. Скорость колеблющейся точки
111. Максимальная скорость колеблющейся точки:
112. Ускорение колеблющейся точки
113. Максимальное ускорение колеблющейся точки
114. Сила, действующая на колеблющуюся материальную точку
115. Полная энергия материальной точки , совершающей гармонические колебания
116. Математическим маятником называется материальная точка, подвешенная на длинной, невесомой и нерастяжимой нити. При выведении из положения равновесия такая система совершает колебания под действием силы тяжести.
117. Период колебаний математического маятника равен
где l -длина математического маятника, g - ускорение свободного падения.
118. Период колебаний пружинного маятника:
где m - масса маятника, k - коэффициент упругости пружины.
119. Затухающими называются колебания, амплитуда которых уменьшается с течением времени.
120. Вынужденными называются колебания, которые происходят под влиянием внешних периодических воздействий. Вынужденные колебания происходят с частотой внешних периодических воздействий.
121. Автоколебания - это незатухающие колебания, существующие за счёт постоянного источника энергии, который периодически включается и выключается самой колебательной системой в нужные моменты времени для пополнения запаса энергии.
122. Резонанс - это явление резкого возрастания амплитуды вынужденных колебаний, когда частота внешних периодических воздействий совпадает с частотой собственных колебаний колебательной системы.
123. Волна - это процесс распространения колебаний в материальной среде.
124. Фронт волны - это поверхность, которая отделяет область пространства, уже вовлечённую в волновой процесс, от области пространства, в которой колебания ещё не возникли.
125. Волновой поверхностью называется геометрическое место точек, колеблющихся в одинаковой фазе.
126. Волны называют поперечными , если колебания в них происходят перпендикулярно направлению распространения волны.
127. Волны называют продольными , если колебания в них происходят вдоль направления их распространения.
128. Поперечные волны распространяются только в твёрдых телах и вдоль границ раздела сред с различными физическими свойствами, например, на границе между водой и воздухом (на поверхности воды), т.к. за механизм их возникновения ответственна деформация сдвига, которая возможна только в твёрдых телах или на границе раздела сред, обладающей упругими свойствами. Примером поперечных волн могут служить электромагнитные волны, волны на поверхности воды.
129. Продольные волны могут существовать в любых средах, т.к. за механизм их возникновения ответственна деформация растяжения-сжатия, которая может возникать в любых средах. Примером продольных волн могут служить звуковые волны в воздухе.
130. Расстояние, на которое распространяется волна за один период называется длиной волны . Или другое определение: кратчайшее расстояние между точками, колеблющимися в одинаковой фазе, называется длиной волны .
131. Волны, частота которых лежит в диапазоне от 16 Гц до 20 кГц, называются звуковыми или акустическими.
132. Скорость звука в воздухе порядка 340 м/с. Она изменяется в зависимости от температуры, плотности, влажности, атмосферного давления. Чем выше плотность среды, тем больше скорость звука. Например, в твёрдых телах она составляет тысячи м/с.
133. Громкость звука зависит от амплитуды колебаний частиц в волне. Чем больше амплитуда колебаний, тем выше громкость звука.
134. Высота тона зависит от частоты. Чем выше частота, тем выше тон.
135. Принцип суперпозиции волн: при распространении в среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частиц среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов.
136. Когерентность - согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов.
137. Когерентные волны - это волны одинаковой частоты, разность фаз которых в процессе распространения остается постоянной во времени.
138. Интерференция волн - сложение когерентных волн, при котором в разных точках пространства получается устойчивая картина усиления или ослабления амплитуды результирующей волны.
139. Условия интерференционных максимумов: разность хода волн равна чётному числу длин полуволн или целому числу длин волн.
140. Условия интерференционных минимумов: разность хода волн равна нечётному числу длин полуволн.
где r - разность хода волн, - длина волны, k = 0,1,2,...
141. Разность фаз двух когерентных волн в данной точке
где r 1 и r 2 – расстояния точки от источников когерентных волн; r 2 -r 1 =r - разность хода волн.
142. Инфразвук - волны с частотами меньше 16 Гц.
143. Ультразвук - волны с частотами больше 20 кГц.
144. Интенсивность звука - величина, определяемая средней по времени энергией, переносимой звуковой волной за 1 с через площадку 1 м 2 , перпендикулярную направлению распространению волны.
II семестр
Механические колебания и волны
Общая черта колебательных процессов – высокая степень повторяемости процесса.
Колебания подразделяются:
по природе: механические, электромагнитные;
по степени повторяемости: периодические, непериодические;
по свойствам: гармонические, ангармонические;
по способу возникновения: свободные, вынужденные.
Механические колебания
Колебательные системы
Колебания – физические процессы, которые происходят с определённой повторяемостью во времени.
Периодические колебания – колебания, при которых значения характерных параметров системы повторяются через равные промежутки времени.
Полное колебание – процесс, проходящие в системе за период.
Период – минимальный период времени, через который все параметры системы повторяются.
Частота – число полных колебаний, происходящих в единицу времени.
Циклическая частота – число полных колебаний за единиц времени.
Гармонические колебания – колебания, происходящие по закону изменения гармонических функций.
Линейные колебания – колебания, возникающие в линейных системах.
Линейная система – система, реакция которой линейно зависит от воздействия.
Свободные (собственные) колебания – колебания, которые происходят в отсутствие внешних воздействий на колебательную систему и возникают вследствие какого-либо начального отклонения этой системы из состояния её устойчивого равновесия под действием внутренних сил системы.
Вынужденные колебания – колебания, возникающие в какой-либо системе под влиянием переменного внешнего воздействия.
Равновесие в механических системах и возникновение колебаний
Условие равновесия точечного
тела:
,
протяжённого тела:
,
.
Характерным свойством колебательной системы является наличие возвращающей (квазиупругой) силы.
,
;
.
Необходимое условие колебательной
системы:
.
Достаточность:
.
Свободные незатухающие колебания
Пружинный маятник:
,
,
,
,
где
.
Математический маятник:
.
,
.
,
,
,
,
,
,
где
.
Физический маятник:
,
,
,
,
,
,
,
где
.
Приведённая длина физического
маятника – длина математического
маятника, период колебаний которого
равен периоду колебаний физического
маятника,
.
Центр качания – математическая точка, отстоящая от точки подвеса на приведённую длину и лежащая на маятнике.
Если физический и математический маятники с приведённой длиной колеблются около одной оси, то материальная точка математического и центр качания физического маятника движутся синхронно, если вначале их отклонили на одинаковый угол и одновременно отпустили.
Точка подвеса и центр качания обратимы (можно подвесить за любую из них, период колебаний будет одинаков).
Уравнение колебаний
Все системы описываются
уравнением
,
где
(пружинный),
(математический),
(физический).
Переменная колебаний – параметр, характеризующий отклонение системы от положения равновесия. (x ).
Решение уравнения колебаний.
Линейный гармонический осциллятор – любая колебательная система, в которой возникают малые линейные гармонические колебания.
Основные характеристики гармонических колебаний
Амплитуда – максимальное
значение переменной колебания
(максимальное отклонение системы от
положения равновесия). Амплитуда всегда
положительна.
,A
– амплитуда.
Фаза – параметр, характеризующий
относительное значения отклонения
системы от положения равновесия (
).
Начальная фаза – значение
фазы в начальный момент времени (
).
Период:
,
частота
,
- циклическая частота.
Свойства гармонических колебаний:
Частота и период гармонических колебаний определяются свойствами самой системы.
Амплитуда и начальная фаза зависят от способа возбуждения колебаний.
Период и частота не зависят от амплитуды.
Скорость и ускорение при колебаниях:
Пусть
.
Тогда,
.
Начальные условие – задание смещение и скорости в начальный момент времени.
Задание начальных условий определяет амплитуду и начальную фазу.
Кинетическая и потенциальная энергия системы:
.
Для пружинного маятника
- закон сохранения энергии при свободных
незатухающих колебаниях.
.,.
Э
нергия
и вычисление периода колебаний:
Представление колебаний с помощью векторных диаграмм и комплексных чисел.
П
усть,
где
.
Возьмём
,
.
Тогда
,
а уравнение
описывает движение проекций конца
вектора по соответствующим осям. Пусть
теперьxy
– комплексная плоскость. Тогда
.
Фазовая плоскость
(пространство) – геометрический образ,
представимый множеством состояний
системы
или
.
Фазовая точка – точка фазовой плоскости, определяемая скоростью и координатой и соответствующая определённому состоянию системы.
Фазовая траектория – линия, которую описывает точка на фазовой плоскости при изменении состояния системы.
Фазовый портрет маятника
– фазовая траектория маятника:
или
(
или 
).
Ф
азовый
портрет для гармонических колебаний:
.
Свободные затухающие колебания
Пружинный маятник:
.,
где
- параметр (коэффициент) затухания,
.
Математический маятник:
.
Решение уравнения свободных затухающих колебаний:
Предположим, что
.
Тогда
,
.
,.
Отсюда.
Обозначив
,
получим:
- решение уравнения свободных затухающих
колебаний.
Если трение мало
,
то
.
Основные характеристики затухающих колебаний.
В
ремя
релаксации – время, в течение которого
значение параметра убывает вe
раз:
.
Декремент затухания
характеризует, во сколько раз амплитуда
колебаний убывает за один период:
.
Логарифмический декремент
затухания характеризует, во сколько
раз изменяется логарифм убывания
амплитуды:
.
Пусть
и совершаетсяN
колебаний, т.е.
.
Тогда
,
.
Скорость и ускорение
затухающих колебаний:
,,.
Добротность системы
.
Э
нергия,
.
.
При
.
Вынужденные колебания
Д
ля
пружинного маятника:
,
гдеm
– масса тела, F
– амплитуда силы,
- циклическая частота
силы.
Для математического маятника:
.
Длительность переходного режима совпадает со временем релаксации.
- амплитудно-частотная характеристика
вынужденных колебаний,
- фазо-частотная характеристика
вынужденных колебаний.
Общее уравнение: , где первое слагаемое представляет собой начальное колебаний системы, которое из-за затухания постепенно сходит на нет, а второе – установившийся режим вынужденных колебаний.
Резонанс.
Н
айдём
максимум амплитуды колебаний в зависимости
от частоты воздействующей силы. Для
этого решим уравнение
.
Получим:
.
Резонанс – явление резкого
возрастания (убывания) амплитуды
вынужденных колебаний при стремлении
частоты воздействия внешней силы к
частоте собственных колебаний (точнее,
к величине
,
где
- коэффициент затухания, но обычно
).
Резонансная частота – частота внешней возбуждающей силы, при которой достигается максимум амплитуды вынужденных колебаний.
Наложение колебаний
Сложение колебаний одного направления
Пусть
,.
Тогда.
Векторная диаграмма:
,
,
.
Тогда
,
Таким образом, .
Б
иения:
Рассмотри два колебания:
и,
где
.
Результирующее колебания будет
описываться уравнением
.
Частота биения:
,
период
.
Взаимно перпендикулярные колебания
Рассмотрим два колебания,
происходящие во взаимно перпендикулярных
направлениях:
,
.
Фигура Лиссажу - эта линия, которую описывает тело, одновременно колеблющееся в двух взаимно перпендикулярных направлениях.
Свойства фигур Лиссажу:
Механические волны
Распространение волн в упругой среде
Волны – процесс распространения колебаний в пространстве с течением времени.
Упругие волны – волны, распространяющиеся в упругой среде.
Волновая поверхность – геометрическое место точек среды, колеблющихся в одной фазе.
Волновой фронт – поверхность, разделяющая возмущённую и невозмущённую части среды.
Виды волн:
Поперечные – колебания в которых происходят поперёк направления распространения.
Продольные – колебания в которых происходят вдоль направления распространения.
В газообразной и жидкой среде колеблется плотность или, что то же, давление. В твёрдой среде и на границе раздела фаз – деформация или, что то же, механическое напряжение.
Волновое уравнение
И
сследуем
колебания струны. Пусть в какой-то момент
времени струна деформирована так, как
показано на рисунке. Тогда уравнение
движения для этой струны выглядит так:
.
Т.к.
и
,
то
.
Спроектируем это уравнение на ось
:
и на осьz
:
.
Т.к.
и
очень малы, то
,.
Тогда
.
Введём линейную плотность
,
тогда
.
Таким образом мы получили волновое
уравнение поперечной волны:
,
где
.
Волновое уравнение для
продольной волны выглядит так:
,
где
,p
– давление в среде распространения
волны.
Анализ механических волн
Пусть
.
Тогда
,
и
,
,
,
.
Подставим это в волновое уравнение:
.
Общее решение волнового
уравнения:
,
где
и
- произвольные функции.
Гармоническое решение волнового уравнения: .
Период волны
,
фаза волны
.
- фазовая скорость волны.
Длина волны – расстояние,
на которое распространяется волна за
один период,
Волновое число
.
Волновой вектор:
,
сонаправлен с направлением распространения
волны.
Фазовая скорость волны –
скорость, с которой движутся точки
волны, колеблющиеся в одной фазе.
.
Геометрические свойства волн
Для трёхмерного случая
выражение
,
где
- это оператор Лапласа, в декартовой
системе координат
.
Плоские, цилиндрические и сферические волны – волны, волновой фронт которых представляет собой соответственно плоскость, цилиндр и сферу.
В случае плоской волны в
волновом уравнении достаточно заменить
,
т.е.
.
Для цилиндрической волны
или, для гармонических колебаний,
.
Здесь
- проекция волнового вектора на ось
.
Уравнение сферической
волны:
,
.
Здесь
- проекция волнового вектора на
радиус-вектор.
Бегущие и стоячие волны
Если , то направление распространения волны сонаправленно с осьюz . Если же , то направление распространения волны противоположно направлено осиz .
Рассмотрим сложение двух одинаковых волн, двигающихся навстречу друг другу. Т.е. пусть ,. Тогда- уравнение стоячей волны.
Узлы – это точки, амплитуда
колебаний которых равна 0 (т.е.
).
Пучности – это точки,
амплитуда колебаний которых максимальна
(т.е.
).
Длина стоячей волны
.
Гармонические колебания происходят по закону:
x = A cos(ωt + φ 0),
где x – смещение частицы от положения равновесия, А – амплитуда колебаний, ω – круговая частота, φ 0 – начальная фаза, t – время.
Период колебаний T = .
Скорость колеблющейся частицы:
υ
=
= – A
ω
sin (ωt
+ φ 0),
ускорение
a
=
= –
A
ω 2
cos
(ωt
+ φ 0).
Кинетическая энергия частицы, совершающей
колебательное движение: E
k
=
=
sin 2 (ωt
+ φ 0).
Потенциальная энергия:
E
n
=
cos 2 (ωt
+ φ 0).
Периоды колебаний маятников
– пружинного
T
=
,
где m – масса груза, k – коэффициент жесткости пружины,
– математического
T
=
,
где l – длина подвеса, g – ускорение свободного падения,
– физического
T
=
,
где I – момент инерции маятника относительно оси, проходящей через точку подвеса, m – масса маятника, l – расстояние от точки подвеса до центра масс.
Приведенная
длина физического маятника находится
из условия: l
np
=
,
обозначения те же, что для физического маятника.
При сложении двух гармонических колебаний одной частоты и одного направления получается гармоническое колебание той же частоты с амплитудой:
A = A 1 2 + A 2 2 + 2A 1 A 2 cos(φ 2 – φ 1)
и
начальной
фазой:
φ =
arctg
.
где А 1 , A 2 – амплитуды, φ 1 , φ 2 – начальные фазы складываемых колебаний.
Траектория результирующего движения при сложении взаимноперпендикулярных колебаний одной частоты:
+
–
cos
(φ 2
– φ 1)
= sin 2
(φ 2
– φ 1).
Затухающие колебания происходят по закону:
x = A 0 e - β t cos(ωt + φ 0),
где β – коэффициент затухания, смысл остальных параметров тот же, что для гармонических колебаний, А 0 – начальная амплитуда. В момент времени t амплитуда колебаний:
A = A 0 e - β t .
Логарифмическим декрементом затухания называют:
λ
= ln
= βT
,
где
Т
– период колебания: T
=
.
Добротностью колебательной системы называют:
Уравнение плоской бегущей волны имеет вид:
y = y 0 cos ω(t ± ),
где у – смещение колеблющейся величины от положения равновесия, у 0 – амплитуда, ω – круговая частота, t – время, х – координата, вдоль которой распространяется волна, υ – скорость распространения волны.
Знак «+» соответствует волне, распространяющейся против оси X , знак «–» соответствует волне, распространяющейся по оси Х .
Длиной волны называют ее пространственный период:
λ = υ T ,
где υ –скорость распространения волны, T –период распространяющихся колебаний.
Уравнение волны можно записать:
y = y 0 cos 2π (+).
Стоячая волна описывается уравнением:
y
= (2y
0
cos
)
cos ωt.
В скобки заключена амплитуда стоячей волны. Точки с максимальной амплитудой называются пучностями,
x п = n ,
точки с нулевой амплитудой – узлами,
x у = (n + ) .
Примеры решения задач
Задача 20
Амплитуда гармонических колебаний равна 50 мм, период 4 с и начальная фаза . а) Записать уравнение этого колебания; б) найти смещения колеблющейся точки от положения равновесия при t =0 и при t = 1,5 с; в) начертить график этого движения.
Решение
Уравнение колебания записывается в виде x = a cos(t + 0).
По
условию известен период колебаний.
Через него можно выразить круговую
частоту
=
.
Остальные параметры известны:
а) x = 0,05 cos(t + ).
б) Смещение x при t = 0.
x
1
= 0,05 cos=
0,05
=
0,0355 м.
При t = 1,5 c
x 2 = 0,05 cos( 1,5 + )= 0,05 cos = – 0,05 м.
в
)
график функцииx
=0,05cos
(t
+
)
выглядит следующим образом:
Определим положение нескольких точек. Известны х 1 (0) и х 2 (1,5), а также период колебаний. Значит, через t = 4 c значение х повторяется, а через t = 2 c меняет знак. Между максимумом и минимумом посередине – 0 .
Задача 21
Точка совершает гармоническое колебание. Период колебаний 2 с, амплитуда 50 мм, начальная фаза равна нулю. Найти скорость точки в момент времени, когда ее смещение от положения равновесия равно 25 мм.
Решение
1 способ. Записываем уравнение колебания точки:
x
= 0,05 cos
t
,
т.
к.
=
=.
Находим скорость в момент времени t :
υ
=
= – 0,05
cos
t.
Находим момент времени, когда смещение равно 0,025 м:
0,025 = 0,05 cos t 1 ,
отсюда cos t 1 = , t 1 = . Подставляем это значение в выражение для скорости:
υ
= – 0,05
sin
=
–
0,05
=
0,136 м/c.
2 способ. Полная энергия колебательного движения:
E
=
,
где а – амплитуда, – круговая частота, m – масса частицы.
В каждый момент времени она складывается из потенциальной и кинетической энергии точки
E
k
=
,
E
п
=
,
но k
= m
2 ,
значит, E
п
=
.
Запишем закон сохранения энергии:
=
+
,
отсюда получаем: a 2 2 = υ 2 + 2 x 2 ,
υ
=
=
=
0,136 м/c.
Задача 22
Амплитуда гармонических колебаний материальной точки А = 2 см, полная энергия Е = 3∙10 -7 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F = 2,25∙10 -5 Н?
Решение
Полная
энергия точки, совершающей гармонические
колебания, равна:
E
=
.
(13)
Модуль упругой силы выражается через смещение точек от положения равновесия x следующим образом:
F = k x (14)
В формулу (13) входят масса m и круговая частота , а в (14) – коэффициент жесткости k . Но круговая частота связана с m и k :
2
=
,
отсюда
k
= m
2
и F
= m
2 x
.
Выразив m
2
из
соотношения (13) получим:
m
2
=
,
F
=
x
.
Откуда
и получаем выражение для смещения x
:
x
=
.
Подстановка числовых значений дает:
x
=
= 1,5∙10 -2
м
= 1,5 см.
Задача 23
Точка участвует в двух колебаниях с одинаковыми периодами и начальными фазами. Амплитуды колебаний А 1 = 3 см и А 2 = 4 см. Найти амплитуду результирующего колебания, если: 1) колебания происходят в одном направлении; 2) колебания взаимно перпендикулярны.
Решение
Если колебания происходят в одном направлении, то амплитуда результирующего колебания определится как:
где А 1 и А 2 – амплитуды складываемых колебаний, 1 и 2 –начальные фазы. По условию начальные фазы одинаковы, значит 2 – 1 = 0, а cos 0 = 1.
Следовательно:
A
=
=
=
А
1 +А
2
=
7 см.
Если колебания взаимно перпендикулярны, то уравнение результирующего движения будет:
cos(
2
–
1)
= sin 2 (
2
–
1).
Так
как по условию 2
–
1
=
0, cos
0 = 1, sin
0 = 0, то уравнение запишется в виде:
=0,
или
=0,
или
.
Полученное
соотношение между x
и у
можно
изобразить на графике. Из графика видно,
что результирующим будет колебание
точки на прямой MN
.
Амплитуда этого колебания определится
как:
A
=
=
5 см.
Задача 24
Период затухающих колебаний Т =4 с, логарифмический декремент затухания = 1,6 , начальная фаза равна нулю. Смещение точки при t = равно 4,5 см. 1) Написать уравнение этого колебания; 2) Построить график этого движения для двух периодов.
Решение
Уравнение затухающих колебаний с нулевой начальной фазой имеет вид:
x = A 0 e - t cos2 .
Для подстановки числовых значений не хватает величин начальной амплитуды А 0 и коэффициента затухания .
Коэффициент затухания можно определить из соотношения для логарифмического декремента затухания:
= Т .
Таким
образом
=
=
= 0,4 с -1 .
